Inleiding

In de Boekzaal voor januari en februari 1693 vormde het veertiende hoofdstuk een ‘Bekentmakinge aan de liefhebbers der Wiskunde’.¹ Het was een bespreking van Stelkonstige Reeckening van den Regenboog, in 1687 anoniem verschenen bij Levyn van Dyck in Den Haag.² Citerend uit het voorwoord van de uitgave schreef de Boekzaal:

’t Byzonder oogmerk van dien Heer was, den ongeleerden te hulp te komen; navolgende de treffelijke voorbeelden van den Amsterdamschen Heer Burgemeester Hudde, die in zijn verkortinge der vergelijkingen, en vaste en algemeene regels der grootste en der kleinste, den jonge lieden stoffe van nasporinge verschaft heeft, gelijk mede door den beroemden Heere Huigens (den oogappel van alle die gene, die deze konsten beminnen) in verscheide zijner brave schriften is gedaan, en voorhenen door den doorluchtigen Heer Raadspensionaris de Wit in zijn klare beschrijvinge der kegelsneden, en waardye van Lijfrenten tegen Losrenten.

Het is niet alleen interessant dat de Boekzaal het drietal Johannes Hudde, Christiaan Huygens en Johan de Witt in één adem noemt met hun bijdragen aan de nieuwe wiskunde, maar ook dat ze geroemd worden voor het toegankelijk en nuttig maken ervan. Het is precies deze combinatie van geleerdheid en dienstbaarheid die centraal staat in deze bijdrage.

Zoals bekend was Hudde een in zijn tijd gerenommeerd beoefenaar van de wiskunde. Net als Huygens en De Witt was hij gevormd door het onderwijs in de nieuwe meetkunde van Frans van Schooten de jonge in Leiden. Als stadsbestuurder probeerde hij zijn kennis nuttig voor de samenleving te maken. Dat was meer dan het toepassen van abstracte methoden en inzichten; de wiskunde had een diepere betekenis voor hem en zijn geestverwanten. Deze bijdrage gaat in op de vraag welke plaats de wiskonsten innamen in leven en werk van Hudde. Startpunt vormt Huddes scheepsmeting uit 1671, gevolgd door een overzicht van zijn wiskundige bezigheden en een schets van zijn stijl van werken. Op basis hiervan bespreek ik de manier waarop hij de wiskunde inzette tijdens zijn bestuursperiode, om tot slot een vergelijking te maken met andere wiskundige heren uit de Gouden Eeuw.

‘Een volmaeckte wijze’

De scheepsmeting van Hudde is te vinden in de Scheeps-bouw van zijn neef Nicolaas Witsen uit 1671. Hudde had hem het betoog schriftelijk meegedeeld, aldus Witsen, die het opnam in het zeventiende hoofdstuk van zijn verhandeling. Dit hoofdstuk bestond uit een ‘wiskonstige betooginge’ over de waterdruk tegen de scheepswand. Aan de hand van de Beghinselen des Waterwichts van Simon Stevin werkte Witsen een hydrostatische analyse uit van de waterverplaatsing door een schip. Dit kwam neer op de toepassing van de wet van Archimedes op grote, drijvende lichamen met een gekromd omhulsel. De ‘volmaeckte wijze’ van scheepsmeting die Hudde had gevonden paste hier uitstekend in.³

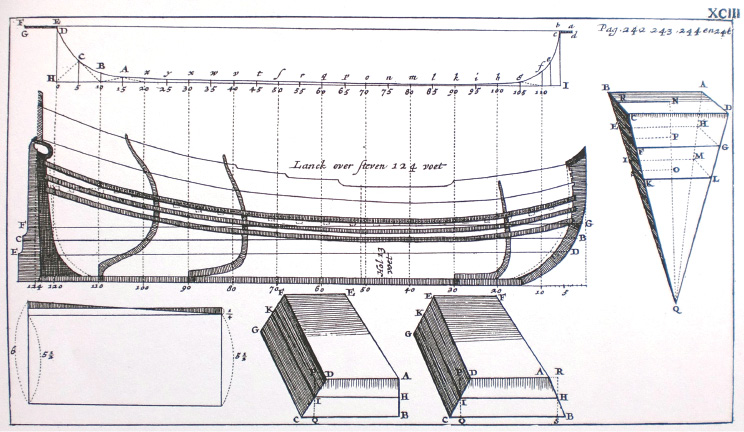
Huddes uiteenzetting was gericht op de vraag hoe de omvang van de vracht van een schip te bepalen was. Met Archimedes – het beginsel ‘dat alle Mathematici in de konst van ’t Water-wicht […] voor axioma gebruiken’ – kwam dit er op neer de omvang van het verplaatste water te bepalen. Hudde gebruikte daarvoor een oriëntatielijn langs de romp die de (gemiddelde) horizontale doorsnede gaf van het lichaam tussen de belaste en onbelaste doorsnede van de scheepsromp. In figuur 1 zijn DE en GF de onder- en bovengrens en BC de ‘lastlijn’:

Zy nu genoomen een Schip na welgevallen […], en gestelt dat het zelve in ‘t Y-water, door zyn volle lading, diep heeft gegaan tot aan de lyn GF toe, en daar na, ontladen zynde, gerezen is tot DE, zynde de hooghte van 6 Amsterdamsche voeten. […] zoo zal het stuk DEFG, tusschen beide uitgesneden, even zoo veel plaats beslaan als het water dat door deeze lading uit zyn plaats is gestooten; en derhalven […] zal het gewight van zoo veel waters, als deeze plaats kan bevatten, gelyk zyn aan de zwaarte van deeze lading.⁴

Om de inhoud van dit lichaam te berekenen moet eerst de omtrek van de romp bepaald worden:

Om welkers inhoudt dan te vinden, zoo span ik een lyn, als, by voorbeeldt, BC, in ‘t midden tusschen DE en EF, dat is hier 3 voet boven de superficie des waters, zoodanig, dat de zelve achter en voor even verre van het midden der steven af staat, en ‘t Schip omtrent op het wydtste raakt. […] Daar na meet ik recht-hoekigh en water-pas van deeze lyn af, […] Concipieert nu dat dit Schip water-pas doorsneden is, gaande de sectie door deeze gespannen lyn, en dat de helft van’t plat dier doorsnyding ons wort vertoont door de figuur a d c e f g h i k l m n o p q r s t u w x y z A B C D G F a, en de gespanne lyn door de rechte IH. Ik begin dan te meeten van achteren by het roer, uit de hoek D, de lengte D o, daar na de lengte C 5, dan B 10, en zoo voorts van 5 tot 5 voet, tot dat ik kome daar de rondte van het Schip tusschen de wydte van 5 voet eenigh aanmerkelyk onderscheidt zoude geven, indien men die zelve rondte voor een rechte lyn quame te nemen, gelyk voor aan de steven gebeurt, alwaar ik van 2 tot 2 voet heb gemeeten.⁵

Op deze manier bepaalde Hudde stap voor stap de doorsnede van het schip bij de gemiddelde lastlijn. Hij ging daarbij niet uitgaat van de breedte van de romp maar van de afstand tussen de romp en de richtlijn HI. Dat was ook praktisch: deze afstanden zijn van buitenaf te meten (fig. 2). Huddes methode was wiskundig superieur voor zijn tijd volgens ingenieur Van Driel, een deskundige op het gebied van tonnenmeting, die in 1924 een historische studie over scheepsmeting publiceerde.⁶ De toen gebruikte methodes gingen uit van de lengte en breedte van de romp en hielden geen rekening met de vorm van het schip.

Hudde onderbouwde de methode met behulp van een uiteenzetting van de hydrostatische uitgangspunten en de meetkundige aanpak. Daarbij ging hij niet alleen theoretisch te werk, maar lichtte het archimedische axioma ook empirisch toe aan de hand van een experiment met een ondergedompelde blaas.⁷ Belangrijker echter was de praktische uitwerking van de methode. Allereerst gaf Hudde in detail aan hoe hij het gewicht van een kubieke voet water bepaalde met behulp van een nauwkeurig gefabriceerd koperen kubusje. ‘Op den 15 Maert’ vond hij: een voet regenwater 45 pond 29 loot, IJwater 46 pond 4½ loot, Texelwater 46 pond 18 loot. Tevens gaf hij aan hoe de opmeting van een schip te corrigeren is voor ongelijkmatig laden van het schip (waarbij voor- of achtersteven dieper in het water komt te liggen) en voor sterk gekromde rompvormen.

Hudde besloot zijn beschouwing met een relativering: ‘ick denk niet dat deze accuraetheit, ten opzigt van de practijck zeer nodig zal zijn’.⁸ Net als bij de bepaling van de brandpuntsafstand in Specilla Circularia volstond bij de bepaling van de waterverplaatsing een ‘mechanische’ waarde.⁹ Het uiteindelijke doel van de methode was efficiëntie en betrouwbaarheid; weliswaar wiskundig onderbouwd, maar in dienst van de praktijk. Die bestond uit een meting langs de waterlijn die, zo stelde Witsen, door twee personen in minder dan twee uur uit te voeren was. De praktische insteek sloot aan bij de benadering van Witsen zelf, die ook wiskundige onderbouwing koppelde aan praktische uitvoerbaarheid. De praktische precisie die tot uitdrukking kwam in Huddes bepaling van het gewicht van verschillende waters, zien we in de vergelijking van het drijfvermogen van zoet, brak en zout water door Witsen: door het verschil in soortelijk gewicht zinken schepen in zoet water meer.¹⁰

Onderhandelingen over tol

De aanleiding van Huddes beschouwing over scheepsmeting was praktisch. Het was bedoeld als bijdrage aan de onderhandelingen tussen de Republiek en Denemarken over tolheffing. Nederlandse schepen moesten tol betalen aan Denemarken, de Sont-tol. De daadwerkelijke afdracht geschiedde in Nederland; schippers kregen een kwitantie mee die ze in Denemarken konden overleggen. De Republiek betaalde de geheven tol uit aan Denemarken, waarbij een deel werd ingehouden in verband met schulden. In 1647 was verdrag gesloten waarbij de tol geheven werd op basis van het laadvermogen van schepen in plaats van de daadwerkelijke lading. De Nederlandse schippers hadden allerlei slimmigheidjes bedacht om belasting te omzeilen, waaronder aanpassing van de vorm van de romp zodat de meting gunstig uitviel. Behalve over deze inkomstenderving ontstond Deense onmin over het feit dat de Republiek meer inhield dan afgesproken. Het conflict verergerde toen de Denen niet langer kwitanties accepteerden en schippers alsnog tol lieten betalen. Dit alles tegen de achtergrond van een algemene verwijdering tussen de twee staten.¹¹

Bij de onderhandelingen over een oplossing voor het conflict werd de methode van scheepsmeting opnieuw bekeken. Bovendien kwam een afgevaardigde uit Denemarken om een neutrale bepaling van het laadvermogen van schepen tot stand te brengen; dat was admiraal Curt Sivertsen Adelaer die vroeg in 1668 arriveerde.¹² In de loop van de onderhandelingen bracht Gilles Valckenier, een vertegenwoordiger van Amsterdam, Huddes methode in. In de diplomatieke stukken van de Deense gezant Poul van Klingenberg is niet alleen een afschrift van de tekst en diagrammen te vinden, maar ook een verslag van een beoordeling van de methode.¹³ Het maakt onderdeel uit van een relaas van de problemen met de uitvoering van een overeenkomst die in februari 1667 gesloten werd. Bij de opmeting en inventarisatie van Nederlandse schepen ontstond onenigheid met de schippers. Op 27 februari was er een bijeenkomst om de problemen te bespreken. Het bleek dat een compromis aangehouden was door de inbreng door Valckenier van de ‘mathematische inventie’ van Hudde. Deze is vervolgens uitvoerig besproken aan de hand van concrete metingen. De aanwezigen hadden een aantal fundamentele bezwaren tegen methode van Hudde: de wiskundige bepaling van de doorsnede van lichaam was niet bruikbaar voor iets onregelmatigs als een scheepsromp; de hydrostatische vergelijking tussen last en waterverplaatsing was niet geldig; de bepaling van het standaardgewicht van IJwater riep twijfels op. De uiteindelijke conclusie luidde, dat ‘de mathematische kunst op het meeten der schepen niet konde passen’. In een missive aan raadpensionaris De Witt vatte Klingenberg op 28 februari de kern samen: ‘hoe qualick de sustenie van den heer Hoddens op het begrooten der schepen lasten kan gepast werden’.¹⁴ De methode van Hudde mag wiskundig beter geweest zijn, in de praktijk overtuigde het niet en zijn voorstel vond geen ingang. Zoals Adelaer, met kennelijke instemming van Michiel de Ruyter, constateerde: ‘Naerdien dat ich well wuste, dat een ding die man tasten ende voelen can ende voor oogen sien veel seecherer ende gewisser is als een aender die alleenlijch bestaet in abstracte mathematische speculatien’.¹⁵ Het uiteindelijke verdrag uit 1669 stelde een praktische methode vast waarbij schepen werden geijkt met een standaardlast van kanonskogels. Per scheepstype werd een vuistregel bepaald voor de diepgang. Witsen besloot het hydrostatische hoofdstuk van de Scheeps-Bouw met een schets van deze methode en haar geschiedenis, alsmede een overzicht van diverse methodes die in andere landen gebruikt werden.¹⁶

De publicatie van de Scheeps-Bouw markeerde een sleutelmoment in de bestuurlijke carrière van Hudde en Witsen. Niet lang daarna, in reactie op de gebeurtenissen van het rampjaar, zouden zij samen met Gillis Valckenier, een andere neef, de bestuurlijke macht in Amsterdam naar zich toetrekken. Op deze manier weerspiegelt Huddes scheepsmeting niet alleen zijn wiskundige vorming, maar ook zijn publieke rol en de inbedding daarvan in de stedelijke politiek. We kunnen wellicht stellen dat er nog een zekere onbekommerdheid uitspreekt: het idee dat diplomatieke geschillen door een rationele, wiskundige aanpak op te lossen zijn.

Hudde was niet de enige die geloofde in de kracht van wiskunde. Een jaar of tien later gaf Ole Rømer in Kopenhagen de Denen advies toen deze nieuwe onderhandelingen initieerden. In oktober 1684 presenteerde hij een methode om de doorsnede van een scheepsromp te benaderen (fig. 3). Hij reageerde rechtstreeks op Huddes verhandeling zoals die in de Scheeps-Bouw was gepubliceerd. Net als bij Hudde werd de fraaie wiskunde van Rømer niet benut door de bestuurders. Rømer had ook wortels in de nieuwe Leidse meetkunde. Zijn schoonvader Erasmus Bartholin had met Van Schooten aan de Geometria gewerkt en hijzelf had tijdens zijn Parijse tijd een hechte band met Huygens opgebouwd. Op deze manier verwijst Huddes scheepsmeting ook naar het internationale netwerk dat zich rond de nieuwe meetkunde ontwikkeld had en waarvan de vertegenwoordigers elkaar op allerlei verschillende manieren tegenkwamen: direct via bezoeken en briefwisselingen, indirect via beschermelingen en betrokkenheid bij bestuurlijke en commerciële projecten.¹⁷

Huddes wiskundige interesses en activiteiten

De scheepsmeting van Hudde mag een nauwkeurige methode zijn geweest voor die tijd, qua wiskunde was het geen uitzonderlijke prestatie. De bepaling van de doorsnede van de romp bestaat uit een meetkundige benadering waarbij de oppervlak onder de kromme op een slimme manier in veelhoeken wordt verdeeld. Nieuwe technieken uit de opkomende analytische meetkunde zijn niet aan de orde. De wiskunde van Rømer was misschien wat hoogstaander; die gebruikte tangenten in plaats van veelhoekige elementjes. De scheepsmeting lijkt op het vroegmoderne landmeten en wijnroeien. Daarmee is er indirect een verband met de nieuwe meetkunde van de zeventiende eeuw: Keplers analyse van het wijnroeien uit 1615 geldt als pionierswerk op het gebied van integraalrekening.¹⁸

Hudde had zijn sporen ruimschoots verdiend in de nieuwe meetkunde en aan die bijdragen is in de geschiedschrijving uitvoerig aandacht besteed. Hoewel het onduidelijk is hoe zijn wiskundige vorming er precies heeft uitgezien en wanneer hij Van Schooten precies heeft ontmoet, staat zijn eerste werk volledig in het teken van de nieuwe meetkunde van Descartes. Al snel maakte hij deel uit van de kring wiskundig angehauchte patriciërszoons rond Van Schooten. Uit 1654 stammen enkele bijdragen, waaronder een analyse van de doorsnede van het folium van Descartes, die werden opgenomen in Exercitationes Mathematicae (1657), een verzameling wiskundige verhandelingen van Van Schooten met een aantal bijdragen van leerlingen. De befaamde brieven die Hudde in augustus 1657 en februari 1658 aan van Schooten stuurde vormden een bijlage in diens grote Geometria uitgave van 1659/60. Naar verluidt zouden deze verhandelingen over ‘verkortinge der vergelijkingen, en vaste en algemeene regels der grootste en der kleinste’ zoals het in de Boekzaal heette, ook uit 1654/5 stammen, iets eerder dan Specilla Circularia. In 1657 nam Hudde deel aan een briefwisseling tussen Huygens, Van Schooten, en René François de Sluse over de analyse van krommen.¹⁹

Volgens Karlheinz Haas is Hudde na 1657, afgezien van een briefwisseling met Huygens over kansrekening in 1663, wiskundig niet meer actief geweest. De historische aandacht voor Huddes wiskunde heeft zich inderdaad beperkt tot zijn ‘geometria’ uit de jaren 1650.²⁰ Als je alleen kijkt naar de ‘zuivere’ wiskunde in de moderne betekenis valt dat te verdedigen, maar dan ga je voorbij aan de bredere betekenis die het begrip ‘wiskunde’ had in de vroegmoderne tijd. Vanuit dat perspectief heeft Hudde na de jaren 1650 nog tal van wiskundige activiteiten ontplooid, om te beginnen in de gemengde wiskunde. Behalve de abstracte kwantiteiten van meetkunde, rekenkunde en algebra behandelde de wiskunde concrete kwantiteiten zoals lichtstraal, snelheid, harmonie, en hemelbewegingen. ‘Toegepast’ wiskundige onderwerpen als optica en statica waren even abstract en formeel als meetkunde en algebra. De verhandeling over de lenzen is een voorbeeld van gemengde wiskunde net als de bijdrage aan het debat over heliocentrisme datzelfde jaar. Huddes interventie was meer astronomisch dan kosmologisch en betrof de vergelijking van de omloopstijd van planeten in verhouding tot de afstand tot de zon.²¹

Hudde gaf een praktische draai aan de wiskundige analyse. In Specilla Circularia betoogde hij dat de sferische aberratie van een lens naar verhouding klein was en concludeerde dat het brandpunt wiskundig gezien weliswaar geen punt was maar in de praktijk wel. Hij noemde het een ‘mechanisch’ punt waarvan de delen niet te onderscheiden zijn. Hiermee onderscheidde hij zich van rigoureuze mathematen zoals Descartes en Huygens, die wiskundig geen onderscheid wensten te maken tussen mathematische en materiële kwantiteiten. In de uiteenzettingen van Witsen en Hudde over waterverplaatsing en tonnage hebben we een vergelijkbaar pragmatisme in de wiskundige analyse gezien. Het onderwerp keerde in 1674 nog even terug. Klaarblijkelijk in reactie op hoofdstuk 17 van de Scheeps-Bouw wisselde Dirk Rembrandtz van Nierop enkele brieven met Hudde, waarvan er één bewaard is gebleven.²² Het bevat een uitvoerige uiteenzetting naar aanleiding van stelling 11 in Stevins Waterwicht over de druk op de wanden van een vat gevuld met vloeistof. Het betrof hier voornamelijk de ‘beghinselen’ van het waterwicht; de stap naar de ‘daet’ van de Scheeps-Bouw wordt niet gezet.

Geluk en lot waren nieuwe onderwerpen van (gemengd) wiskundige studie. Waar Huygens’ ‘Reeckening in Speelen van Geluck’ nog betrekking had op het otium van dobbelende heren, was het negotium van verzekeren en beleggen de inzet van de statistische beschouwingen van Hudde en Johan de Witt. De vraag was wat een goede uitkering was voor een lijfrente; steden en Staten vreesden te veel geld kwijt te zijn. De Witt en Hudde bogen zich er in 1671 over en consulteerden daarbij ook Huygens. Ze bedachten dat de uitkering gerelateerd moest zijn aan de levensverwachting. Naast concepten uit Huygens’ waarschijnlijkheidsrekening waren daarvoor gegevens nodig over de levensduur van burgers. Hudde had toegang tot de Amsterdamse archieven en verzamelde gegevens over de uitkeringen op lijfrentes die door de stad waren verkocht in de periode 1586–1590. Van 1495 personen bepaalde hij de daarna nog geleefde jaren om zo een calculatie te maken van het rendement van de uitgifte. De uiteindelijke voorstellen werden niet geïmplementeerd. Niet omdat ze wiskundig niet overtuigend waren maar omdat het tijdstip verkeerd uitpakte. Rond het rampjaar was de onzekerheid te groot voor ingrijpende veranderingen die wantrouwen bij beleggers konden veroorzaken.²³

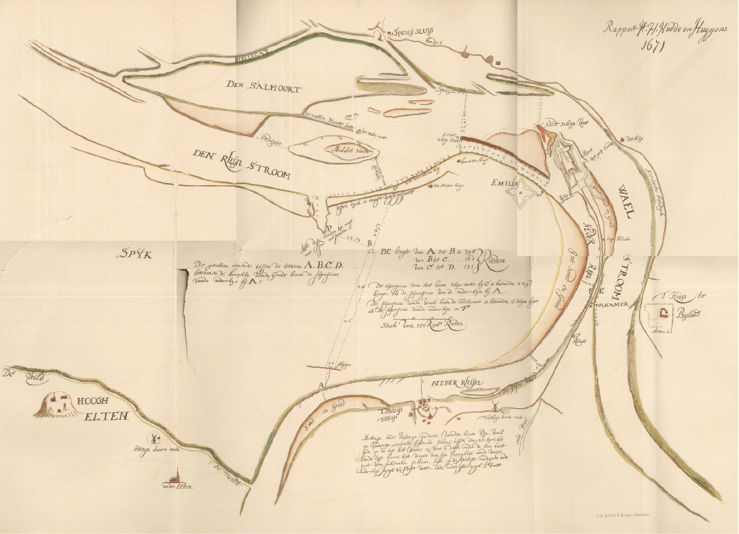
Het lijfrenteproject past bij het civieltechnische advieswerk dat heel gebruikelijk was voor geleerde heren in de vroegmoderne tijd, zoals de beoordeling van voorstellen voor ontzanding, inpoldering, lengtevinding; rapportages over water-, verdedigings-, en andere werken. In 1671 kregen Huygens en Hudde een goedbetaalde opdracht van de Staten-Generaal om de toestand van de Nederrijn en IJssel te inspecteren en advies te geven over mogelijke ingrepen (fig. 4). De watertoevoer naar de Nederrijn was een notoir probleem en de geleerde heren brachten het watersysteem nauwkeurig in kaart, waarbij ze ook metingen deden aan het verval van het water. Met een grieperige brief stuurde Hudde het verbaal en advies naar Huygens waarbij hij ook nog inging op de gedachtewisseling met De Witt over de lijfrenten. Hun conclusie was dat grote ingrepen waarschijnlijk geen structurele oplossing boden; de voorstellen tot bescheiden aanpassingen werden door het rampjaar ingehaald. Overigens was het ook een politiek probleem waarbij belangen tot in Dordrecht meespeelden en de soevereiniteit van provincies in het geding was. Als bestuurder was Hudde ook direct betrokken bij de proeven met Huygens’ uurwerken op VOC-schepen in 1687; hij bracht het onderwerp in bij het bestuur. In 1697 was hij met zijn beschermeling Burchardus de Volder betrokken bij een advies over een voorstel van ene Antonius de Saint-Julien-Poitiers over lengtevinding. In dezelfde lijn zijn adviezen over distillatie van water op VOC-schepen en de teelt van zijdewormen in Holland. Dat brengt ons verder van de wiskunde af; maar het is de vraag in hoeverre in de hoofden van de Gouden Eeuw zo’n onderscheid gemaakt werd.²⁴

Daet bij het wiskonstige woord

Hudde was niet alleen een geleerd heer die op verzoek advies gaf; de scheepsmeting en lijfrenteberekeningen waren eigen projecten en gericht op praktische interventies. Zeker nadat hij stadsbestuurder was geworden initieerde hij tal van projecten rond waterstaatkundige en andere civieltechnische onderwerpen. In het rampjaar 1672 trok de factie van Gilles Valckenier de macht in Amsterdam naar zich toe en verwierf Hudde een centrale rol in het stadsbestuur (zoals bekend bekleedde hij tot 1703 het ambt van burgemeester zo vaak als mogelijk was, twee van elke drie jaren). Theo de Jong en Huib Zuidervaart bespreken Huddes rol in de stadsinrichting elders in dit nummer uitvoeriger, dus ik beperk me tot enkele wiskundige kanten.

Naast de zwakke staat van de vestingwerken werd met de Allerheiligenvloed van november 1675 ook de verdediging tegen het water een acuut probleem. De oplossing, die de toegang tot de haven en het vervoer over de grachten niet belemmerde, bestond uit een versterking van de kade en de aanleg van sluizen in de voornaamste grachten. In 1681 werd het plan aangenomen en Witsen aangesteld als projectleider. Opmerkelijk, want een dergelijk project werd normaliter geleid door de Stadsfabriek, toezichthouder en uitvoerder van publieke werken in de stad. Onderdeel van het plan vormde het beheer van de waterstand op stadsniveau in plaats van wijkniveau. Daartoe werd een stadpeil bepaald op basis van een reeks nauwkeurige metingen van de waterhoogte van de Zuiderzee, een bepaling van de gemiddelde vloedhoogte en gegevens over de waterhoogtes in de diverse buurten. Het peil werd door de hele stad vastgelegd met stenen die in de sluizen werden ingemetseld; van deze zogenaamde Huddestenen bestaat die in de Eenhoornsluis nog. In 1683 werden de werken voltooid en beschermden Amsterdam tot in de achttiende eeuw succesvol tegen overstromingen.²⁵

Een ouder waterprobleem van de stad was de kwaliteit van het water. Door de ligging aan zee en het natte, vlakke ommeland was de doorstroming van de grachten slecht te beheersen. Het was moeilijk schoon water naar de stad te krijgen en het vuile water eruit met als gevolg dat de snel gegroeide metropool waarschijnlijk de smerigste stad van Europa was. Onder leiding van Hudde werd het oude plan weer opgenomen om sluizen in de dam in de Amstel aan te leggen om daarmee gecontroleerd de grachten door te kunnen spoelen. Het plan werd ten uitvoering gebracht maar zonder het verwachte resultaat. Op dezelfde manier had Huddes verbeterde rosmolen weinig effect (fig. 5). Op basis van een analyse van de benodigde arbeid maakte hij more geometrico een optimaal ontwerp dat in 1675 getest werd. De molen werkte naar behoren maar loste het waterprobleem ook niet op. Uiteindelijk boden bestuurlijke maatregelen ten aanzien van afvoer van afval en aanvoer van drinkwater enige soelaas. Al sorteerden zijn wiskundige plannen weinig effect, als bestuurder was Hudde uitgesproken succesvol.²⁶

Maatschappelijk dienstbare wiskunde

Huddes inzet om de infrastructuur van Amsterdam te verbeteren brengt ons bij de vraag naar de betekenis van zijn brede wiskundige belangstelling en de rol ervan speelde in zijn bestuurlijke optreden. Naar aanleiding van het rosmolenontwerp stelt Siger Zeischka dat de meerwaarde van de wiskundige analyse voor het technische resultaat beperkt was.²⁷ In het algemeen kan inderdaad gesteld worden dat dergelijke civieltechnische vraagstukken te complex waren voor een eenduidige wiskundige behandeling en dat geldt ook voor zaken als lengtevinding. Bovendien waren de problemen van meer dan technische aard en de oplossingen voor het belangrijkste deel bestuurlijke kwesties. Het directe nut van de wiskunde in Huddes bestuurlijke projecten was daarom gering. Dat laat echter niet verlet dat hij er belang aan hechtte om onderzoekingen en beschouwingen ‘more geometrico’ in te kleden.

De zeventiende eeuw kan gezien worden als de eeuw van de wiskunde. Op tal van manieren schiepen de wiskundige wetenschappen beloftes van waarheid, nut en aanzien. Niet alleen kregen wiskonstenaars een dominante stem in praktijken van vestingbouw, navigatie, en cartografie; ook verwierf de wiskunde een bepalende plaats binnen de wetenschappen, en een status als sleutel tot rationaliteit. Dit was niet alles onbetwist, maar ontegenzeglijk verwierf de wiskunde een prominente plaats in het vertoog over kennis.²⁸ Het is daarom niet verrassend dat jonge vertegenwoordigers van de burgerij belangstelling toonden voor de nieuwe wiskunde. Dat was niet helemaal zonder dubbelzinnigheden. Enerzijds begonnen de wiskonsten zich te ontworstelen aan de praktische ongeleerde wortels in landmeetkunde, vestingbouw en boekhouden. Daarmee waren ze acceptabel voor een lichtelijk aristocratiserend patriciaat dat een academische scholing tot onderdeel van de opvoeding maakte. Anderzijds raakte die nieuwe elite niet helemaal los van een aardse gerichtheid op nut en profijt. Misschien dat het juist het ambivalente karakter van Descartes’ wiskunde op het grensvlak van algebra en meetkunde was, die het aantrekkelijk maakte voor een De Witt, een Huygens, een Heuraet, een Hudde. Maar misschien was het ook gewoon de rol die sleutelfiguren als Constantijn Huygens speelden. We moeten daarbij niet vergeten dat de jeugdige overgave aan de nieuwe meetkunde van Van Schootens pupillen ook binnen de nieuwe elite tamelijk uitzonderlijk was; wiskunde was en bleef een ‘acquired taste’.²⁹

De Amsterdamse rekenmeester Abraham de Graaf bracht het tweevoudige belang van de wiskunde in 1676 fraai onder woorden. Wiskunde heeft alledaags nut in handel, scheepvaart, vestingbouw, enzovoort; zelfs wanneer dat niet onmiddellijk zichtbaar is. Maar wiskunde heeft ook intellectueel nut: het leert redeneren en oordelen. ‘Het Theoretice brenght de Ziel geen minder nut toe als het practice het lichaem’. Deze woorden komen uit de voorrede van De Geheele Mathesis, een leerboek voor de nieuwe wiskunde dat aansloot bij de opvattingen van de opkomende elite. De nieuwe meetkunde werd naast de klassieke als grondslag gepresenteerd: analytisch en synthetisch. De Graaf presenteerde zich als leermeester van deze bijdetijdse wiskunde, in haar natuurlijke gedaante behandeld, zich daarmee onderscheidend van de gewone rekenmeesters. Het heeft er alle schijn van dat hij zich met de in eigen beheer en zeer verzorgd uitgegeven Geheele Mathesis een positie trachtte te verwerven in de kringen rond Hudde.³⁰

De ‘zuivere’ wiskunde uit zijn studiejaren kun je zien als liefhebberij voor Hudde. Er zaten nuttige kanten aan, voor bijvoorbeeld telescoopbouw, maar ook de dioptrica was in de eerste plaats een bijdrage aan ‘gemengde wiskunde’. De stijl van de Specilla is wat anders dan de Dioptrica waar Huygens in dezelfde periode aan werkte, maar de werken zijn vergelijkbaar in de poging een wiskundige analyse van concrete telescopen te maken. In zijn bestuurlijke werk vanaf de jaren 1660 streefde Hudde daadwerkelijk nut na. Zoals Vermij al opmerkte: deze aristocraat bij uitstek probeerde de wetenschap in dienst te stellen van het algemeen nut.³¹ De lijfrente, scheepsmeting en waterbeheer waren misschien niet direct toepasbaar, maar wel gericht op maatschappelijke ingrepen. De benadering van Hudde was uitgesproken exact, wat tot uitdrukking komt in de abstractie en algemeenheid van het Amsterdamse waterpeil. Het peil was gebaseerd op nauwkeurig meetwerk en werd geïmplementeerd met behulp van een fijnmazig geodetisch netwerk door de stad. De hele stad werd doorsneden door één denkbeeldig vlak waarmee het peil van de Zuiderzee overgebracht kon worden door grachten en straatjes. Daarmee werd het waterpeil door de hele stad heen bijgehouden en konden ingrepen op elkaar afgestemd worden. Het abstracte geodetische vlak maakte op die manier het Amsterdamse waterbeheer tot een stedelijke aangelegenheid.

Het succes van de waterverdediging – in termen van management alsook effectiviteit – wordt vaak toegeschreven aan het specifieke karakter van de groep bestuurders die de leiding had in Amsterdam in het laatste kwart van de zeventiende eeuw. De groep rond Hudde en Witsen had een bijzondere belangstelling voor de nieuwe filosofie, wiskunde, en natuurlijke historie en had nauwe banden met geleerden als Christiaan Huygens, Isaac Vossius, Frederick Ruysch, en Johannes Swammerdam.³² Die voorliefde voor wiskunde en wijsbegeerte zou hun bestuurlijke werk beïnvloeden en een soort ‘scientific management’ opleveren. Het is echter gevaarlijk om een wiskundige aanpak of een filosofische benadering meer rationeel of berekend te noemen dan andere vormen van bestuur. De grote uitleg van Amsterdam zoals die vanaf de late zestiende eeuw haar beslag had gekregen was een zorgvuldig georganiseerd proces van meten, rekenen, en afwegen.³³ De belangrijkste vernieuwing onder Hudde c.s. was de manier waarop de Stadsfabriek omzeild werd en specifieke projectleiders aangesteld. Het feit dat iemand als Witsen het hoogwaterproject aanstuurde duidt eerder op een centralisatietendens ten koste van de expertise van vaklui als de stadstimmerman.³⁴ Zelfs als Huddes benadering rationalistisch was, moet het belang van de nieuwe filosofie niet overschat worden door het te duiden als een soort toepassing van ‘géométrie’ op bestuurlijke vraagstukken. Het is een benadering die door de inzet van wiskundige middelen een indruk wekt van objectiviteit en probleemoplossend vermogen. Daarbij is de zeggingskracht van een uiteenzetting in mathematische stijl binnen het bestuurlijke en politiek debat belangrijker dan de daadwerkelijke antwoorden en uitkomsten.

Wiskonsten voor de stad

Hudde en zijn medestanders mogen zich een rationalistische houding aangemeten hebben, opvallend genoeg werd onder het bewind van zijn factie de ietwat technocratische aanpak van stedebouw en waterstaat niet geïnstitutionaliseerd. In samenspraak met Simon Stevin had Maurits in 1600 een ingenieursschool in de Leidse universiteit geïnitieerd waar vestingbouwers Nederlandstalig onderwijs kregen in de wiskunde, de Duytsche Mathematique. Op dezelfde manier was onder leiding van Adriaan Metius aan de Franeker universiteit wiskundig onderwijs voor ‘idioten’ opgezet. Deze initiatieven weerspiegelden de vernieuwingen die de neven Nassau in de oorlogsvoering hadden doorgevoerd en waarin ingenieurs een prominente rol speelden. Die hadden in hun ogen een adequate, formele vorming nodig naast de opleiding in het veld.³⁵ De benadering van infrastructurele werken van Hudde et al. lijkt op die van de stadhouders aan het begin van de eeuw. Een Amsterdamsche Mathematique – met De Geheele Mathesis als lesboek en De Graaf als hoogleraar – kwam er echter niet. Stedelijke wiskunde werd overgelaten aan de vrije markt van rekenmeesters en navigatieonderwijzers, een drukbezette en sterk competitieve sector in Amsterdam.³⁶ Er was geen gildestructuur en ook de overheid bemoeide zich niet met opleiding, toelating en toezicht, met uitzondering van landmetersexamen op provinciaal niveau. Voor de infrastructurele projecten vertrouwde het stadsbestuur op het gildesysteem van de bouwsector en in het geval van de vestingwerken in 1672 Statelijke ingenieurs. Voor specifieke projecten moest soms een proeve van bekwaamheid gedaan worden of een model bij een aanbesteding.³⁷ Ondanks de omvang en het belang van de stedenbouwkundige activiteiten in de zeventiende eeuw, heeft Amsterdam nooit een instelling opgericht om ambtsdragers, leidinggevenden en uitvoerders op te leiden.

Naast directe toepassingen in handel en bestuur kan geleerdheid ook nuttig gemaakt worden in meer culturele zin, door het in te zetten om het aanzien van de stad te vergroten. De Scheeps-bouw kan gelezen worden als proeve van Amsterdams kunnen en een manier om de reputatie als handelsstad te versterken. Op dezelfde manier publiceerde Witsen in 1687 en 1692 een grote kaart en een uitvoerige beschrijving van Noord en Oost Tartarye.³⁸ Het hielp Amsterdamse ondernemers toegang te krijgen tot Russische heersers om daarmee nieuwe markten te openen. De Witsens zelf profiteerden mee want de familie handelde al sinds het begin van de eeuw op Rusland. Het culturele kapitaal van de nieuwe wiskunde en filosofie werd zo benut als ruilmiddel (‘matter of exchange’, om Cook te citeren).³⁹ In dat licht kan ook het Athenaeum gezien worden als een manier om de geleerde reputatie van de stad te vergroten. Het was een klassieke instelling voor hoger onderwijs gericht op de stedelijke elite – en een instelling waarop ook Hudde invloed uitoefende, zoals bij de benoeming van de cartesiaan Johannes de Raeij in 1669. Het onderstreepte het zelfbewustzijn van een Nederlandse stad als Amsterdam zoals dat ook tot uitdrukking kwam in het chorografische werk van stadsbeschrijvingen en -gezichten.⁴⁰ De meer hoofse benutting van geleerdheid is ook zichtbaar in de manier waarop in de Scheeps-Bouw de praktische en wiskundige behandeling is ingebed in een filologische verhandeling over Archimedes en andere helden uit de Oudheid.

Hudde zelf spreidde zijn geleerdheid als bestuurder minder publiekelijk tentoon dan iemand als Witsen. Zijn jeugdige publicaties waren anoniem of doorgegeven via anderen zoals Van Schooten en Witsen. Zijn intellectuele opvattingen waren slechts indirect zichtbaar, via contacten en verwijzingen. In zijn dissertatie over kometen uit 1662 verwijst Nicolaas Witsen via opdracht en stellingen naar de deskundigheid van Hudde in de optica. Hetzelfde doet Abraham de Graaf door in zijn Geheele Mathesis naar Hudde te verwijzen en diens analyse van lenzen over te nemen.⁴¹ Voor Hudde bleef de wiskunde een liefhebberij, een talent dat op gepaste momenten gebruikt kan worden om het bestuurlijk en politieke verkeer te smeren, maar geen boodschap om uit te dragen.

Zijn collega-burgemeester in Franeker, Bernard Fullenius maakte een radicaal andere keuze. Net als Hudde had Fullenius zich in zijn jonge jaren overgegeven aan de wiskunde. Zijn vader bekleedde de leerstoel aan de universiteit, dus het was hem met de paplepel ingegoten. Fullenius reisde rond, correspondeerde, en legde contacten met geleerden van naam zoals Johannes Hevelius en Jacob Bernoulli. Met een beschouwing over kometen gaf hij rond 1670 een visitekaartje als getalenteerd mathemaat. Toen Bernoulli in 1681 door de Republiek reisde bezocht hij zowel Hudde als Fullenius om van gedachten te wisselen over kometen, en aan hen droeg hij daarna zijn eigen verhandeling over kometen op.⁴² Fullenius was inmiddels burgemeester, net als Hudde; de bekroning van de ambities van de familie. De leerstoel aan de universiteit van de Duitse dominee Fullenius was slechts een opstap voor een grotere toekomst voor de familie. Behalve als Franeker magistraat, bekleedde Fullenius een centrale rol in het Friese netwerk van bestuur en politiek. In 1684 maakte Bernard jr. echter een onverwachte stap. Hij deed afstand van zijn positie als magistraat en verwierf de positie van hoogleraar aan de Franeker academie. Bezien vanuit een Hudde was het een ongehoorde stap, terugtrekken in de academie en een verlies van macht en invloed, en daarmee de mogelijkheid om het vertrouwen in het nut van het wiskundig denken in de praktijk te brengen.

In hetzelfde jaar als de Boekzaal de lof citeerde voor Huddes maatschappelijk dienstbaar maken van geleerdheid, bracht de jonge David Gregory een bezoek aan de Amsterdamse bestuurder.⁴³ Hudde vertelde hoe hij als jongeling vrijwel onmiddellijk in de nieuwe meetkunde gedoken was en met Van Schooten problemen uitgewisseld had en nieuwe methodes ontwikkeld. Met De Witt had hij zich gebogen over wat hij beschouwde als het moeilijkste probleem, de bepaling van het aantal krommen van het tweede geslacht (die Hudde beperkte tot derdegraads). En hij haalde zijn constructie voor een bladvormige kromme aan, die Van Schooten in 1657 opgenomen had in zijn Exercitationes. Allemaal herinneringen aan een ver verleden, het liefhebberen in de geometria had Hudde al lang achter zich gelaten.