The effect of perturbations on resistance to sliding in second-order moments comparing two different bracket types
- 1Department of Orthodontics, School of Dentistry, Faculty of Medicine & Dentistry, Edmonton Clinic Health Academy, University of Alberta, Edmonton, AB, Canada
- 2Department of Mechanical Engineering, University of Alberta, Edmonton, AB, Canada
- 3School of Dentistry, Faculty of Medicine & Dentistry, Edmonton Clinic Health Academy, University of Alberta, Edmonton, AB, Canada
- Paul W Major, School of Dentistry, Faculty of Medicine & Dentistry, 5478 Edmonton Clinic Health Academy, University of Alberta, 11405-87 Ave NW, Edmonton, AB T6G 1C9, Canada. Email: major{at}ualberta.ca
Abstract
Orthodontic literature has shown all ligation methods to behave similarly in the clinical situation; however, the reasoning behind this still requires further investigation. A novel frictional device able to measure forces at the level of the bracket along with a custom perturbation device was used to investigate the effect of perturbations on resistance to sliding (RS) using conventional and passive ligated brackets. 150 3M Victory Series twins (0.022 slot) and 150 Damon Q brackets (0.022 slot) were tested using an 0.018 x 0.025 stainless steel wire for RS. There were 5 test groups consisting of equal numbers (n=30) representing combinations of high and low amplitude and frequency of perturbations along with a control. Second order angulation tested ranged from 0 to 6 degrees. Results for conventional brackets in the presence of perturbations at 0 degrees showed there was a statistically significant reduction (P<0.001) in RS when compared to controls. At 6 degrees, this difference (P<0.001) was seen in both high perturbation groups and one of the low perturbation groups. For passive ligated brackets, no statistically significant difference between groups was seen at 0 degrees. However, at 6 degrees high perturbation groups both resulted in statistically significant (P<0.001) reductions in RS when compared to controls. From this study it was concluded that passive ligated brackets have a lower RS when compared to conventional ligated brackets under all test conditions and angulations. Also, amplitude of perturbations has a larger role than frequency in reduction of RS values.
Introduction
Friction and resistance to sliding (RS) are topics that have been well studied within the orthodontic literature. Kusy and Whitley define RS as a combination of classical friction, binding or notching depending on the contact angle.1 In terms of this research terminology, classical friction is defined as the friction resulting from the active ligation method pressing the archwire against the bracket slot base. The contact angle is the angle between the archwire and the bracket slot during second-order rotations or tipping.2 The critical contact angle (θc) is the angle at which the archwire makes initial contact with the opposite corners of the bracket slot wall, and it is at this angle that binding begins.2 Binding represents friction resulting from the force couple within the bracket as the archwire engages the corners of the bracket slot wall. As θ ≥ θc, the friction associated with this wire and bracket slot wall interaction begins to play a larger role in RS than classical friction. If the contact angle exceeds what Kusy and Whitley refer to as θz, then notching occurs.2 Notching refers to the phenomenon where there is permanent deformation and interlocking of materials. Notching, when present, dominates over classical friction with respect to RS.1,2
The only systematic review on the frictional resistance of passive versus conventional brackets concluded that passive ligated systems show lower friction with round wires, relatively aligned segments, and the absence of tipping or torqueing moments.3 It would seem intuitive that passive ligated systems would be beneficial in situations where minimal friction is desired such as during initial leveling and aligning. This is due to free movement of the wire inside the bracket being allowed, as the ligation method does not actively engage the two. Likewise, higher friction is desired during anchorage or finishing and detailing, which may benefit from conventional ligated systems as a result of the ever-present archwire and bracket engagement. That is, the archwire will at the very least be engaged with the ligation elastics which will exert a vertical force on the archwire. A variety of in vivo studies have been conducted which suggest that the ligation method does not influence treatment outcome.4⇓⇓–7 This may be explained by the strengths of each system: passive ligated brackets may treat initial stages quicker while conventional ligated brackets may be more efficient in the latter stages resulting in similar overall treatment time. Another proposed explanation is that small vibrations or perturbations temporarily reduce the RS, possibly allowing both systems to operate similarly.8 Intra-orally, these perturbations may be of small magnitude resulting from talking or breathing, or of large magnitude from bruxism and mastication.
In vivo studies regarding the impact of ligation method on clinical outcome are necessary to understand the reality of orthodontic appliances; however, they do not allow for the strict control of many variables (e.g. perturbation magnitude or frequency, temperature, etc.). While acknowledging limitations in matching the clinical situation, in vitro experiments allow for strict control of experimental variables. Thus, in fully understanding the causality of similarities in ligation methods, it is necessary to isolate the impact of single variables and use these results in conjunction with in vivo studies.
Research studies related to the role of perturbations in RS have only surfaced within the last 15 years,9⇓⇓⇓–13 and none have compared active and passive ligation while varying the contact angle and subjecting the system to perturbations. The aim of this study is to investigate and quantify the effect of perturbations on RS while varying the bracket–archwire second-order contact angle. Additionally, force measurements in all three dimensions will be quantified at the location of the bracket allowing for determination of RS values. Both frequency and amplitude of vibration will be varied in order to understand whether one has a more significant effect on RS over the other.
Materials and methods
Maxillary left canine (#2.3) brackets were selected to simulate canine retraction during space closure. Unitek Victory Twin Series 0.022-in slot brackets (3M Unitek, Monrovia, CA) were selected to represent conventional ligated brackets, and Damon Q (Ormco, Orange County, CA) 0.022-in slot brackets were selected to represent passive ligated brackets. Bracket widths were 0.127 and 0.110 in for the 3M and ORMCO series, respectively, as specified by the manufacturers. The θc as defined by Kusy and Whitley for the conventional bracket was 1.81° and 2.08° for the passive ligated bracket.2 The wire used in all test conditions was a 0.018 × 0.025 stainless steel wire (Ormco, Orange County, CA). Stainless steel wire was selected for this experiment as this is the material typically used for sliding mechanics due to the fact that it has the lowest coefficient of friction among the materials used in orthodontic wires.14 Wire dimension was selected as per previous published work and protocol by Fathimani.15
A medium effect size and power of 0.8 was selected for this study leading to a minimal sample size of 28 per test condition as per Table C.4 provided by Portney and Watkins.16 We incorporated two additional tests per group in case of bracket failure (e.g. debond), for a final sample size of 30 per test group. There were a total of four test conditions and a control for both conventional ligated and passive ligated brackets resulting in a total sample size of 300.
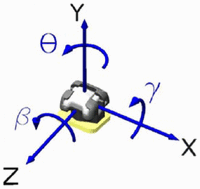
Brackets were mounted to custom cut metal dowels. The Damon Q brackets used in this experiment had a preprogramed 7° of torque. In order for the bracket to sit perpendicular to the long axis of the dowel, a 7° offset was cut into the dowel, functionally transforming the torque to 0°. Conventionally ligated brackets did not have a torque prescription and thus did not require customized dowels. Each bracket–dowel unit was numbered and randomly assigned into one of the test groups. The bracket–dowel combinations were each individually imaged in three planes using a charge coupled device (CCD) camera (Bausch & Lomb, Rochester, NY) under magnification and analyzed using a custom image measuring program written in MATLAB (Mathworks, Natick, MA) to determine orientation in three dimensions. This program allows for identification of the offset from the center of the dowel in the x-, y-, and z-axes as well as any rotations around these axes identified by angles θ, β, and γ (Figure 1). Using a transformation matrix, measurements are made at the load cell and translated to the location of the bracket.17
Diagramatic view of the x-, y-, z-axes orientated to bracket as well as angles θ, γ, β (note: the bracket depicted is not meant to represent a particular type or design, and is only provided to aid in placing the coordinate system).
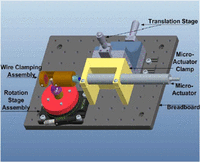
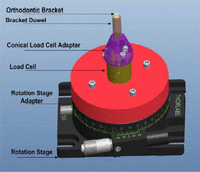
A custom three-dimensional (3D) frictional (Figures 2 and 3) device was designed. The conical load cell adaptor connects the load cell with the test bracket dowel. Both the bracket–dowel sample and conical load cell adaptor have a flat edge which allows reproducible orientations on separate tests. The load cell (Nano 17 SI-50-0.5, ATI Industrial Automation, Apex, NC) is mounted to a programmable micro-adjusting rotating platform (Precision Rotation Platform, PR01, Thor Labs, Newton, NJ) which when turning reproduces second-order movements in the x–z plane. This particular load cell is capable of measuring forces up to 50 N in the x- and z-directions with a resolution of 1/80 N, and up to 70 N in the y-direction with the same resolution. When considering moments, it can measure up to 500 N mm in all three directions with a resolution of 1/16 N mm. There are also two manual translation stages (1/2-in Translation Stage, MT1, Thor Labs, Newton, NJ) that allow for micro-adjustments in the y- and z-axes to allow proper positioning of the wire into the bracket slot. That is, initially, the wire will not engage with the bracket slot. The wire is secured into a programmable linear micro-actuator (M230.10 DC-Mike Actuator, Physik Instrumente (PI) GmbH&Co, Karlsruhe, Germany) which allows the operator the ability to pull the wire along the x-axis at a consistent and constant speed. The micro-actuator and rotating platform are operated by calibrated custom software so that programmed test conditions were exactly repeatable for each bracket.
Parameters of the experiment such as speed of pull, rate of sampling, averaging of samples, and amount of rotation are predetermined by the investigator and inputted into the software using a configuration file. Each individual bracket–dowel combination will have a unique configuration file with these parameters along with its specific offsets. θ was tested between 0° and 6° in 1° increments. Load cell data were collected at a sampling rate of 4000 Hz. Data collection occurred over a total distance of 0.2 mm at each angle increment with the wire speed set at 0.05 mm/s.
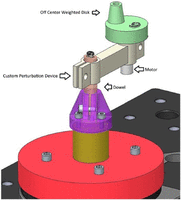
A custom perturbation device was designed (Figure 4). The device is composed of a rotating motor along with custom designed weighted disks. The weighted disks designed to fit on the head of the rotating motor have off center weights that create imbalance and vibrations when spun. As the weight is moved farther away from the center of the disk, rotation causes greater perturbation amplitude. The rotating motor is run by a function generator (GW Instek GFG-8216 A, New Taipei, Taiwan) monitored by an oscilloscope (Tektronix TDS 2024B, Beaverton, OR) and a custom-built 5 V power supply. By adjusting the duty cycle on the generator and the amount and offset of weight in the disks, the device can create distinct combinations of frequency and amplitude of perturbations. The device is mounted directly to the test dowel so that perturbations are delivered at the source which simulates force on a tooth. Perturbations generated by this device were felt at the location of the bracket along the x- and z-axes of the bracket, that is, in the mesial-distal and axial directions of the tooth with no labial-lingual component.
The load cell is able to measure 3D forces and moments. As the bracket begins to tip and contact is established with the wire, forces are created along the x- and z-axes with little influence in the y-axis. As the critical contact angle is reached and exceeded, contact forces at opposite ends of the bracket produce an increasing couple in the y-direction of the bracket. Force components related to RS are along the x- and z-axes, so that the resultant force representing the RS is
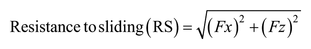
For each individual randomized test, the bracket–dowel complex was mounted to the load cell. The custom perturbation device was secured so that it was flush to the dowel surface and perpendicular to the bracket slot. The appropriate sized perturbation disk was selected and secured to the rotating motor head. The 0.018 × 0.025 stainless steel wire (Ormco, Orange, CA) was secured to the micro-actuator and using the translation stages the wire was positioned over the bracket slot. With the aid of a Bausch & Lomb microscope (Bausch & Lomb, Rochester, NY) and the micro-adjustments on the rotating platform, the bracket slot was lined up parallel to the wire so that equal space existed above and below the wire. The wire was also set so that it was not contacting the bracket base prior to ligation. In the passive ligated system, the gate was closed. In the conventional ligated bracket, a standard elastomeric ligature (silver color power O modules, size 0.120, Ormco, Orange, CA) was used to secure the wire to the bracket. To ensure that elastomeric ligatures were stretched the same amount and that no distortions or twisting occurred when securing the bracket wings, a straight shooter ligature gun (TP Orthodontics, La Porte, IN) was used.
The desired perturbation conditions were then set for the bracket being tested. Table 1 provides the description of the test conditions with respect to amplitude and frequency of perturbations. Initial testing was done to determine the amount of force that the perturbations would deliver by measuring the forces and moments at the level of the bracket without a wire. Because the perturbations were generated by a rotating disk, the force pattern was cyclical. Averaging these values resulted in a net effective force of 0. Instead, the root mean squared (RMS) value was used to establish the force value of the perturbations. Several combinations of rotating wheels and frequencies were tested and final test conditions were chosen based on similar force-RMS values with different frequencies. Because of the relatively slow (compared to the rate of data acquisition from the load cell) cyclical nature of the perturbation, the rate of sampling allows enough time that the force associated with the perturbations averages out to 0, leaving only the force associated with RS. The amplitude chosen for both low and high perturbation group consisted of force levels which are within the range (0.7–1.2 N) recommended for tooth translation.18 Based on limitations of the equipment (primarily dynamic range of the load cell), it was not possible to replicate amplitudes associated with processes such as mastication; however, this range is indicative of tooth movement, and would form the lower bound for which perturbations could be expected to influence RS.
Description of the test conditions with respect to amplitude and frequency of perturbations.
Although data-sets were collected and presented for seven different angulations (0°–6°), we chose to only report statistics at 0° and 6°. These two angles represent angles that are well below and well above the critical contact angle. The data were first tested using repeated measures analysis of variance (ANOVA) for main effects and interactions. For post hoc testing, angulation was fixed and bracket type and test condition were investigated with separate two-way ANOVA. When comparing bracket type, α = 0.05. Because there were four planned comparisons between the test conditions and to prevent inflation of type I error rate, the Bonferroni (multiple-comparison) correction was applied and α was divided by 4 resulting in α = 0.05/4 = 0.0125.
Results
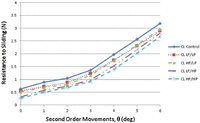
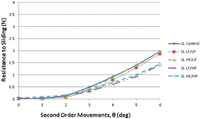
The relation between RS and tip angle for the two ligation methods and various perturbation conditions are shown in Figure 5 (conventional ligation) and Figure 6 (passive ligation).
Graph of second-order movement versus resistance to sliding for conventional ligated (CL) brackets.
LF: low frequency; HF: high frequency; LP: low perturbations; HP: high perturbation.
Graph of second-order movement versus resistance to sliding for passive self-ligated (SL) brackets.
LF: low frequency; HF: high frequency; LP: low perturbations; HP: high perturbation.
As mentioned above, statistical analysis was performed at two tip angles (above and below the critical angle for the onset of binding). Table 2 presents mean RS for test groups, mean difference in RS for test groups compared to controls for conventional and passive ligated brackets at 0°. At fixed angulation of 0°, there was a statistically significant reduction in RS (p < 0.001) between all test conditions compared to control for conventional ligated brackets. By determining the reduction in amplitude of RS between test conditions and control, we are able to calculate the percentage reduction in RS due to perturbations. For conventionally ligated brackets, high perturbation resulted in a 59% (0.367 N/0.628 N) and 50% (0.311 N/0.628 N) reduction in RS (high frequency and low frequency respectively). For passively ligated brackets, no significant reductions in RS were found.
Table of mean resistance to sliding (RS) for test groups, mean difference in RS for test groups compared to controls for conventional and passive ligated brackets at 0°, P-values, and 95% confidence intervals.
Table 3 presents mean (RS) for test groups, mean difference in RS for test groups compared to controls for conventional and passive ligated brackets at 6°. For conventional ligated brackets at fixed angulation of 6°, three of the four tested conditions resulted in a significant (p < 0.001) reduction in RS. Once again, the largest reduction was seen in the high perturbation groups resulting in 16% (0.495 N/3.18 N) and 12% (0.381 N/3.18 N) (high frequency and low frequency respectively). For passive ligated brackets, reduction in RS only occurred with the high perturbation test conditions resulting in reductions of 27% (0.526 N/1.971 N) and 28% (0.569 N/1.971 N) (high frequency and low frequency respectively).
Table of mean resistance to sliding (RS) for test groups, mean difference in RS for test groups compared to controls for conventional and passive ligated brackets at 6°, p-values, and 95% confidence intervals.
At angulations tested, there was a significant (p < 0.001) difference in RS between conventional and passive ligated brackets. Conventional ligated brackets displayed higher RS when compared to passive ligated brackets under all test conditions. The smallest difference between these two bracket types occurred under the high perturbation test conditions (Figures 5 and 6).
As expected, current results show that the presence of perturbation decreases RS for all conditions. Figure 5 shows that for conventional ligation, the reduction in RS is fairly uniform at all tip angles and a higher perturbation level increases the magnitude of the reduction. Frequency of the perturbation does not seem to be significant in these tests. Figure 6 shows that for high amplitude perturbations in passive self-ligation above the critical tip angle (approximately 2°), the reduction in RS increases with increasing tip angle. For self-ligated (SL) brackets, amplitude of perturbation seems to play a stronger role than frequency, at least for the conditions tested.
Discussion
Experiments done by previous investigators using different methodologies all seem to come to the same conclusion: perturbations reduce the RS.9⇓⇓⇓–13 This study provides a reproducible and accurate quantification of the effect of perturbation on RS for two common designs of conventional and passive SL brackets. In addition, the influence of amplitude and frequency of vibration are considered to understand which dominates in regards to their impact on RS values.
From the results, it is evident that there is greater RS using a conventional ligated bracket compared to a passive ligated bracket under any perturbation test condition or angulation. This is the result of the additional friction within the bracket wire interface caused by the force from the elastic ligation, either pushing the wire into the back of the slot or by direct contact (“grabbing the wire”). As angulation increases and surpasses the critical contact angle, friction due to ligation plays a smaller role in RS when compared to the friction associated with binding and notching (due to bracket and wire design).1,19 Perturbations of any amplitude or frequency reduce the RS when using a conventional ligated system; however, larger reductions were seen in test groups that utilized high amplitude perturbations.
Because passive systems are designed to produce minimal to no resistance when θ < θc, perturbations were not expected to have much effect at these angles. A cautionary note must be included here that an idealized scenario was generated in this study whereby the archwire did not initially engage the bracket. This was done intentionally such that the frictional resistance solely due to second-order angulation could be identified; however, in a clinical scenario, it is likely that sources of resistance due to misalignments on other axes (e.g. first or third order rotations) may be present and generate friction. Thus, it should not necessarily be assumed, based on these results, that passively ligated brackets do not generate friction when θ < θc. It was observed that for passive brackets when θ > θc, perturbations of high amplitude independent of frequency produced a reduction in RS where low amplitude perturbations did not. Although high amplitude perturbations have the largest effect on RS for both conventional and passive ligated brackets at both tested angulations, there was a larger net reduction in passive ligated brackets at 6°. The data for this experiment suggest that amplitude of perturbations may have a more significant role in reducing RS than frequency, and that higher perturbations are more effective than lower levels of perturbation.
An inherent limitation to this study based on experimental equipment was the inability to maintain the same low and high frequency of vibration for both levels of perturbation; however, while this is indeed a limitation, it also helps to support the notion that amplitude of vibration plays a larger role than frequency. The high and low frequencies of the low and high perturbations, respectively, are very similar in magnitude. With this being the case, if there is no significant difference from the mean at one scenario but there is at another, it can reasonably be suggested that perturbation was the cause. For example, when studying RS values for passive ligation at 6° of rotation in Table 3, it can be seen that the low perturbation high frequency case was not statistically different from the mean; however, the high perturbation low frequency scenario was statistically different. The fact that the frequency did not remain consistent for the levels of perturbation tested is a limitation that should be remedied in future work, yet when viewing the results in this light it aids in further supporting conclusions.
This particular result provides a better understanding of the similarities between passive and active ligation in the clinical scenario. While the tested force range of perturbation is significant enough to generate movement in the system, forces well over 100 N may be obtained which would produce more tooth movement than in this study.20 Based on the trend observed here, it can be suggested that with additional amplitude of perturbation the RS would continue to decrease regardless of the frequency. In such a case, especially for low contact angles, it is certainly possible that typical daily activities could cause a reduction in RS to negligible values allowing for archwire movement. It is not suggested that vibration is the sole cause of similarities between the types of ligation tested here; however, it can be seen as a significant contributing factor.
The wire was pulled at a rate of 0.05 mm/s, which is significantly faster than what is seen clinically (1 mm/month = 3.8 × 10−7 mm/s). Therefore, it is important to consider the time scale carefully when designing the experiment. Perturbations must be delivered at a higher frequency to compensate for the faster rate of wire pull in order to keep ratios of perturbations per mm movement consistent. Perhaps a more meaningful way of describing the rate of perturbations is to measure the number of perturbations per millimeter of wire movement, rather than the number of perturbations per second. By measuring the rate of perturbations in this manner, the speed at which the wire was pulled would no longer be a factor. Experiments would have to be conducted to determine the speed of tooth movement as well as the rate of perturbation events intra-orally to determine this relationship.
Caution must always be exercised when conferring results from in vitro studies to an in vivo model. The oral environment is extremely complex, and although our experiment is able to account and measure several factors previously not quantified (e.g. forces and moments in all three directions), it still represents a simplified model. Because of the variability of frequency and amplitude of bite force in individuals, a limitation of this study was the determination of the test groups for perturbations used in this study. The biology and physiology of teeth and bone are also factors which are difficult to control. Teeth and bone are not as rigid as metal dowels, and the effect of periodontal ligament space is difficult to reproduce accurately in the lab setting. 3M Victory Twin type (3M, Monvrovia, CA) bracket was used to represent a typical conventional ligated bracket and Damon Q (Ormco, Orange, CA) bracket was used to represent a typical passive ligated bracket. Although clinically, this represents a good representation of a conventional versus passive bracket, it does introduce variables such as bracket design which have to be considered. Because brackets were not retested in this experimental design, individual bracket differences due to manufacturer tolerances may introduce some variability in the data.
Conclusion
RS is higher in conventional ligated when compared to passive ligated brackets in the presence and absence of perturbations. Greater reductions in RS are seen using higher amplitude perturbations in both conventional and passive ligated systems suggesting that amplitude may play a larger role in reducing RS than frequency. While the range of frequencies and amplitudes tested did not reduce the RS entirely to zero for all contact angles, it can be suggested that this would certainly be achievable at lower angles for both methods of ligation. This in vitro study aids in understanding the causality for conventional and passive ligation methods leading to similar clinical outcomes.
Article Notes
-
Declaration of conflicting interests The authors declare that there is no conflict of interest.
-
Funding This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
- Received January 21, 2014.
- Accepted September 29, 2014.
- © The Author(s) 2014
This article is distributed under the terms of the Creative Commons Attribution-NonCommercial 3.0 License (http://www.creativecommons.org/licenses/by-nc/3.0/) which permits non-commercial use, reproduction and distribution of the work without further permission provided the original work is attributed as specified on the SAGE and Open Access page (http://www.uk.sagepub.com/aboutus/openaccess.htm).